FOR-LOOPS IN MATHEMATICS
It is possible to roughly divide programming language theorists into to two groups: advocates of imperative-style programming, and advocates of functional-style programming.
Members of the latter group often deride the former for its presumed inelegance and disorderliness. In one such example, in the abstract of his 1984 paper Why Functional Programming Matters, John Hughes, now a professor at the Swedish Chalmers University of Technology, stated "conventional [imperative] languages place conceptual limits on the way problems can be modularised" and "function languages push those limits back."
While members of the functional group have made important contributions to programming language theory and real-world applications, it is intellectually dishonest to completely forsake all imperative approaches to problem-solving the way that its most fervent supporters do. J.R.R. Tolkien wrote that "courage is found in unlikely places." Similarly, I posit that imperative lines of thought can yield elegant solutions, even in a place as inconducive to disorderliness as mathematics.
To demonstrate my point, consider a mathematical concept similar to for-loops of imperative programming lagnuages: summation notation.
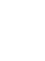
The above expression yields the same result as the final value of s in this imperative Go code:
s := 0
for i := 0; i <= 10; i++ {
s += i
}
Can difficult problems in mathematics be solved with an imperative approach without sacrificing elegance?
First, examine probability problems involving discrete random variables. Surely, discrete problems will lend themselves well to an imperative approach, given the introduced summation notation.
On a given school day, little Bobby must choose between olive slacks, khakis, and brown corduroys. He selects the olive slacks with probability 1/3, the khakis with probability 1/6, and the brown corduroys with probability 1/2. After choosing which pair of pants he is going to wear, Bobby selects his shirt. Since it's not true that all his shirts look just as good with corduroys as they do with khakis, and so on, Bobby's choice of shirt depends somewhat on his choice of pants. The probability he chooses a light green shirt is 3/4, given he has already chosen to wear khakis, and 1/8 each, given he has chosen to wear one of the other two pairs of pants. (It's a shame corduroys don't go with more outfits, isn't it?)
The probability, P(g), that Bobby wears a light green shirt to school on any given day is simply the sum of the probabilities of him choosing the light green shirt, given his pants selection, for each pair of pants. For each! Your imperative senses should be tingling right now. We can write this down using summation notation:
But is it possible to extend the imperative approach to problem solving beyond discrete probability problems? Some would think the answer is certainly "no." After all, since there is no concept of a continuous data type, at least at the computer architecture level of any digital computer, it should be a fool's game to attempt to solve mathematics problems dealing with continuous numbers through the lens of imperition [sic]. I say the formula for learning is a valliant attempt paired with a discerning eye when things start to break down. What exactly breaks down when this approach is applied to problems with continuous numbers?
Pick three random real numbers from the uniform distribution U(0, 1). What is the probability, P(x + y + z < 1), their sum is less than 1? Follow the imperative line of thought I proposed for finding the probability Bobby wears a light green shirt on a given school day. P(x + y + z < 1) is simply the probability of choosing a number z < (1 - (x + y)) for all y for all x, given x + y < 1. For all.
Summation notation does, indeed, describe "for all values in this set, plug the value into this expression; finally, return the sum." So why doesn't it work here? It doesn't work because there is an implicit assumption that the set contains discrete values, not continuous. Luckily, the beloved concept "for all values in my provided set, together with my provided expression, give me a number" has been extended to support intervals—an interval is the set of all real numbers between two of them—and has already been studied for centuries. Another name for this concept is the definite integral. Finding P(x + y + z < 1) is now as simple as writing down and evaluating some definite integrals.